Написание кода

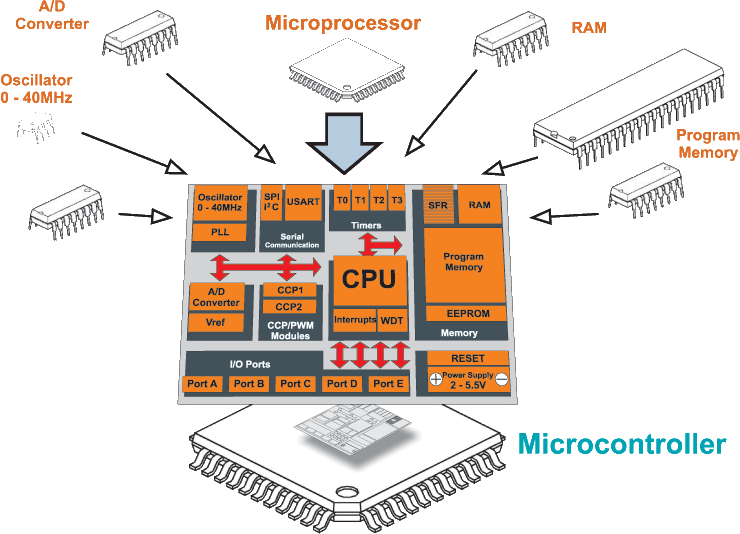
Разработав функциональную схему устройства, собрав электронную схему и написав алгоритм работы, можно приступать к написанию кода для микроконтроллера. Начнем с первого примера (учебного).

Контроллеру необходимо выводить на семисегментном индикаторе цифры. Семисегментный индикатор представляет собой матрицу из семи светодиодов, размещенных таким образом, чтобы зажигая их в разных сочетаниях, можно было бы отобразить любую десятичную цифру, а также специальные символы. Кроме этого индикатор дополняется еще одним сегментом, который предназначен для отображения десятичной точки. Подключение одного семисегментного индикатора и управление им с помощью микроконтроллера – процедура несложная. Для этого достаточно сегменты индикатора подключить к порту микроконтроллера через токоограничительные резисторы по 150 Ом. Общий вывод подключить к линии другого порта. В зависимости от того какую цифру надо вывести, в порт выводим двоичный код этой цифры, ссылаясь на тип подключенного индикатора (с общим анодом или катодом) на общий провод подаем плюс или минус. Для удобства можно сделать таблицу кодов для индикатора (таблица 22).

Таблица 22. Таблицакодов для индикатора

Каждый раз по прерыванию мы должны в обработчике сначала погасить индикаторы, затем выбрать из заранее подготовленного массива выводимых символов очередной символ, вывести его в порт и включить индикатор. Так мы можем менять символы на индикаторе.

Фрагмент кода программы для определения таблицы символов имеет вид:

;Массив с кодами цифр

jmp m1

table:

db 00111111b;0

db 00000110b;1

db 01011011b;2

db 01001111b;3

db 01100110b;4

db 01101101b;5

db 01111101b;6

db 00000111b;7

db 01111111b;8

db 01101111b;9

db 01110110b;H

Чтение данных происходит от клавиатуры. Рассмотрим, как должен считывать данные с клавиатуры контроллер. При использовании большого количества кнопок управления целесообразно применить матричную схему подключения клавиатуры, сходную с приведенной на рисунке 27. В данной схеме 12-ти клавишная клавиатура 4´3 соединяется выводами с портом ввода/вывода P3. Причем, линии 4-6 порта P3 настроены как выходные и обозначаются соответственно PORTE.4 – PORTE.6, а линии 0 – 3 – как входные (PINE.0 – PINE.3). Горизонтальные линии матрицы через токоограничительные резисторы подключены к положительному полюсу источника питания (+5 В).

Рис. 27. Принципиальная схема подключения матричной клавиатуры к микроконтроллеру

Нажатие одной из клавиш замыкает в соответствующей позиции горизонтальную и вертикальную сигнальную линии. Если на вертикальную линию был подан уровень напряжения, соответствующий “логическому нулю”, то при нажатии клавиши на горизонтальной линии также установится низкий уровень напряжения. Алгоритм опроса нажатия клавиши сводится к поочередной установке низких уровней напряжения на вертикальных линиях (PORTE.4 – PORTE.6) матрицы (см. временные диаграммы управляющих сигналов на рис. 28) и считывании информации об уровне сигнала на горизонтальных линиях (PINE.0 – PINE.3).

Рис. 28. Временные диаграммы сигналов на выходных линиях (PORTE.4 – PORTE.6)

Рассмотрим пример проверки нажатия одной из клавиш первого и второго (крайних справа) столбцов матричной клавиатуры, схема подключения которой приведена на рис 27:

. . .

ldi R19,0b11110000//Загрузить константу F0h в R19;

ldi R20,0b11100000Загрузить константу Е0h в R20;

ldi R21,0b11010000загрузить константу D0h в R21;

ldi R22,0b00001111загрузить константу 0Fh для маскирования в R16;

out 02,R19настройка линий E0-3на ввод, а E4-7 –на вывод;

lbl1:метка перехода для повторения опроса;

out 03,R20установить в 0 уровень напряжения на линии PORTE.7, соответствующей первому столбцу клавиатуры;

nopустановить задержку в один такт;

in R17,01считать данные из регистра PINE в R18;

out 03,R21установить в 0 уровень напряжения на линии PORTE.6, соответствующей второму столбцу клавиатуры;

nop установить задержку в один такт;

in R18,01считать данные из регистра PINE в R18;

and R17,R22обнулить неинформативную старшую тетраду в R17;

and R18,R22обнулить неинформативную старшую тетраду в R18;

cp R17,R22сравнить значение в регистре R17 со значением 0Fh;

brne lbl2выполнить переход на метку lbl2, если R18 ≠ 0Fh (одна или несколько клавиш первого столбца клавиатуры нажаты);

cp R18,R22сравнить значение в регистре R18 со значением 0Fh.

brne lbl2выполнить переход на метку lbl2, если R18 ≠ 0Fh (одна или несколько клавиш второго столбца клавиатуры нажаты);

rjmp lbl1переход на метку lbl1 для повторения процедуры опроса;

lbl2:метка выхода из процедуры опроса.

. . .

Если в результате процедуры опроса в битах младших тетрад регистров R17 и/или R18 будут находиться 0, то это будет свидетельствовать о нажатии клавиш, позиции которых можно определить исходя из схемы, изображенной на рис. 27, и номеров обнуленных разрядов в тетрадах.

Рассмотрим код реального устройства.

Данные измерений датчиков можно считывать как из регистров хранения, так и пользоваться функциями FIFO. Имеется отдельный регистр под названием Who am I, значение, записанное в этом регистре постоянно и его можно только считать, можно использовать как идентификатор устройства, значение в регистре 104 или 0х68. Отдельным выводом является выход прерываний, который настраивается регистрами настройки под определенные события.

Датчики гироскопа и акселерометра изготовлены как MEMS (микроэлектромеханическая система) - внешнее воздействие на датчик сначала изменяет состояние механической части, затем изменение состояния механической части приводит к изменению сигнала электрической части. Одним словом в одном корпусе собрана не только электроника, но и механика. В микросхеме MPU6050 содержится сразу два MEMS датчика, производитель утверждает, что их взаимное воздействие друг на друга сведено к минимуму.

Разберемся, как можно использовать датчики акселерометра и гироскопа. Гироскоп выдает значения мгновенной угловой скорости с разрешением, заданным в настройках, например 2000 градусов в секунду. Если прошить микроконтроллер и смотреть на получаемые данные, то увидим только нули. Если начать крутить датчик, то получим мгновенные значения угловой скорости. Заметьте, что скорость мы получаем в градусах в секунду, а это значит, что линейные скорости не влияют на эти показания - показания будут изменяться только при повороте датчика в пространстве. Далее с помощью этих данных можно получить ориентацию объекта в пространстве. Для этого нужно получить мгновенное значение угловой скорости и умножить его на промежуток времени между опросами датчика гироскопа. Пример разрешение 2000 градусов в секунду, промежуток между опросами датчика 0,1 секунда, значение мгновенной скорости 300, значит 300*0,1=30 - за это время ось гироскопа была повернута на 30 градусов. Далее каждое полученное значение нужно сложить с предыдущим. Если ось двигалась в одном направлении - значение 30 градусов, если в другом, то -30, таким образом, при возвращении датчика в исходное положение всегда (в идеале) будет 0, при отклонении от исходного положения, при выполнении вышеописанных действий, получим угол отклонения. Обрабатывая углы трех осей гироскопа можно получить ориентацию объекта в пространстве.

Таким образом, при интегрировании состояния угла положения, также интегрируется и погрешность - при длительном использовании можно получить уже абсолютно неправильные значения. Поэтому часто гироскоп используют в паре с акселерометром, образуя в простом варианте альфа-бета фильтр или комплементарный фильтр.

С акселерометром все проще. Измеряя ускорения трех осей датчика можно получить данные, преобразуя их с помощью геометрии, по которым можно также получить ориентацию объекта в пространстве. Помимо этого акселерометр измеряет линейные ускорения, то есть ориентация объекта может искажаться при движении датчика в линейных направлениях. Также с помощью акселерометра можно определять движение объекта или его столкновение. Например, детектировать падение объекта или толчок о преграду, чтобы обходить это.

Данные от акселерометра получаем всегда достаточно точные, то есть нуль всегда остается нулем ни при каких воздействиях (имеется ввиду не зависит ни от времени, ни от характера воздействия), Однако недостаток кроется в том, что данные идут шумом в некотором диапазоне данных, то есть до десятых долей градуса точно измерять угол не получится. Зато исходя из экспериментальных данных, точность до целых значений градуса держится вполне стабильно. Не забываем про влияние линейных ускорений.

Если датчик приобрели, можно переходить к рассмотрению внутренностей модуля, а именно главного элемента - микросхемы MPU6050. Информация хранится в регистрах микросхема, которых более 100. И вот тут то и кроется огромный подводный камень. производитель не утрудился расписать в документации всю информацию, а привел лишь информацию о самом необходимом. На самом деле не известно даже сколько же всего там регистров, доступных для чтения или записи или того и другого. Также информации на некоторые регистры попросту нет, кроме его названия. Ну что же, придется экспериментально определять влияния значений, записанных в некоторые регистры.

Интерфейс I2C работает по стандартной схеме. Адрес микросхемы может быть двух значений (без бита чтения / записи) в зависимости от состояния вывода AD0 - b1101000, если AD0 соединен с землей и b1101001, если AD0 соединен с источником питания. Соответственно плюс бит чтения или записи.

Микросхема содержит Digital Motion Processor (DMP), он необходим для того, чтобы обрабатывать данные, получаемые из датчиков гироскопа и акселерометра. Все это делается для того, чтобы повысить точность получаемых данных, так как пр обработке данных на микроконтроллере точность может пострадать из-за снижения скорости их обработки. Как правило, алгоритмы обработки движения должны работать с достаточно высокой частотой, обычно 200 Гц, как утверждает документация.

Что касается регистров, то их достаточно большое количество, необходимая информация находится в карте регистров на MPU6050.

Короткий пример эскиза-это очень короткий эскиз и он показывает все исходные значения (акселерометр, гироскоп и температуры).

// MPU-6050 Short Example Sketch

#include<Wire.h>

const int MPU=0x68; // I2C address of the MPU-6050

int16_t AcX,AcY,AcZ,Tmp,GyX,GyY,GyZ;

void setup(){

Wire.begin();

Wire.beginTransmission(MPU);

Wire.write(0x6B); // PWR_MGMT_1 register

Wire.write(0); // set to zero (wakes up the MPU-6050)

Wire.endTransmission(true);

Serial.begin(9600);

}

void loop(){

Wire.beginTransmission(MPU);

Wire.write(0x3B); // starting with register 0x3B (ACCEL_XOUT_H)

Wire.endTransmission(false);

Wire.requestFrom(MPU,14,true); // request a total of 14 registers

AcX=Wire.read()<<8|Wire.read(); // 0x3B (ACCEL_XOUT_H) & 0x3C (ACCEL_XOUT_L)

AcY=Wire.read()<<8|Wire.read(); // 0x3D (ACCEL_YOUT_H) & 0x3E (ACCEL_YOUT_L)

AcZ=Wire.read()<<8|Wire.read(); // 0x3F (ACCEL_ZOUT_H) & 0x40 (ACCEL_ZOUT_L)

Tmp=Wire.read()<<8|Wire.read(); // 0x41 (TEMP_OUT_H) & 0x42 (TEMP_OUT_L)

GyX=Wire.read()<<8|Wire.read(); // 0x43 (GYRO_XOUT_H) & 0x44 (GYRO_XOUT_L)

GyY=Wire.read()<<8|Wire.read(); // 0x45 (GYRO_YOUT_H) & 0x46 (GYRO_YOUT_L)

GyZ=Wire.read()<<8|Wire.read(); // 0x47 (GYRO_ZOUT_H) & 0x48 (GYRO_ZOUT_L)

Serial.print("AcX = "); Serial.print(AcX);

Serial.print(" | AcY = "); Serial.print(AcY);

Serial.print(" | AcZ = "); Serial.print(AcZ);

Serial.print(" | Tmp = "); Serial.print(Tmp/340.00+36.53); //equation for temperature in degrees C from datasheet

Serial.print(" | GyX = "); Serial.print(GyX);

Serial.print(" | GyY = "); Serial.print(GyY);

Serial.print(" | GyZ = "); Serial.println(GyZ);

delay(333);

}

Комплементарный фильтр

Подсистема стабилизации – очень важный компонент любого беспилотного летательного аппарата или балансирующего робота. Именно этот блок машины позволяет ей всегда оставаться в заданном положении, несмотря на действие различных внешних сил.

Для того чтобы осуществить эту стабилизацию, машина должна:

• определить углы наклона платформы относительно поверхности земли;

• вычислить отклонение платформы от требуемого положения;

• подать управляющие сигналы для активации, для компенсации отклонения и приведения платформы в требуемое положение.

Первую задачу решает прибор, называемый инклинометром. Третью задачу — контроллер или регулятор.

Гироскоп

Самый простой инклинометр может быть сконструирован либо с помощью гироскопа, либо с помощью акселерометра. В первом случае угол наклона устройства легко вычисляется с помощью дискретного интегрирования скорости его вращения, определяемого именно гироскопом.

Однако, у MEMS гироскопа есть один коварный недостаток, который называется дрейфом нуля. Суть этого недостатка сводится к тому, что при остановке вращения гироскопа, он все еще будет показывать значение отличное от нуля. Другим недостатком такого решения, является применение процедуры дискретного интегрирования, которая по своей природе дает неточный результат. Третья проблема тесно связана с предыдущей. Она выражается в постепенном накоплении ошибки вычисления угла из-за ограниченной точности переменных микроконтроллера.

Какой же вывод можно сделать из сказанного выше? А такой, что если строить инклинометр только на основе гироскопа, он будет довольно неточен. Значит и стабилизация машины будет весьма посредственная.

Акселерометр

Если мы конструируем инклинометр с помощью акселерометра, то для определения угла наклона достаточно применить простые геометрические преобразования к его показаниям. Акселерометр позволяет определять точные углы наклона прибора только в состоянии покоя. Пока на него не действуют внешние силы, на выходе прибора мы получим значение проекции ускорения свободного падения на наблюдаемую ось. На рис. 29 показания акселерометра для одной из его осей отмечены буквой X. Зная G и X, можно вычислить угол отклонения акселерометра от горизонтального положения – a;

sin(a) = X/G; a = arcsin(X/G).

Делая такие вычисления, важно учитывать, что X и G должны измеряться в одинаковых единицах. Например, если показания акселерометра вы преобразуете к единицам гравитации, другими словами G = 1 земная гравитация, то выражение для угла a примет вид:

a = arcsin(X).

Рис. 29. К расчету угла наклона

Таким образом, на основе одного только акселерометра можно также достаточно легко построить инклинометр. Но, к сожалению, любое воздействие внешней силы вносит в эти вычисления ошибку. Такой внешней силой может быть, например, вибрация от двигателей БПЛА или внезапный порыв ветра. Частично снять это воздействие можно с помощью ФНЧ, но побочным эффектом подобной обработки сигнала будет сильное уменьшение быстродействия инклинометра.

В итоге у нас имеется два замечательных прибора, каждый из которых позволяет рассчитать углы наклона платформы относительно поверхности земли. Но в случае гироскопа точность таких расчетов снижается из-за дрейфа нуля и ошибок интегрирования. В случае же акселерометра слишком велика чувствительность к внешним воздействиям.

Возникает естественное желание объединить показания этих двух устройств для устранения их недостатков. Сделать такое объединение позволяет комплементарный фильтр, работа которого определяется достаточно простым выражением:

a = (1-K)*gyr + K*acc

Здесь

a — отфильтрованный, результирующий угол наклона;

gyr и acc — значения угла наклона, полученные при помощи гироскопа и акселерометра;

K — коэффициент комплементарного фильтра.

Как видно, итоговая величина угла наклона представляет собой сумму интегрированного значения гироскопа и мгновенного значения акселерометра. По сути, главная задача комплементарного фильтра здесь в том, чтобы нивелировать дрейф нуля гироскопа и ошибки дискретного интегрирования. Указанное выражение именно это и делает. На каждом шаге интегрирования (по сути шаге цикла управления платформы) мы корректируем интеграл угла наклона с помощью показаний акселерометра. Сила же этой коррекции определяется коэффициентом фильтра K.

Выбор коэффициента K зависит от величины дрейфа нуля гироскопа, от скорости накопления ошибок вычисления и от условий использования машины. Так, слишком большое значение K приведет к тому, что на результат работы фильтра будет сильно влиять вибрация корпуса БПЛА. Слишком же малое значение K может оказаться недостаточным, чтобы ликвидировать дрейф нуля гироскопа. Как правило, коэффициент комплементарного фильтра подбирается вручную для каждого инклинометра исходя из вышеуказанных условий.

Таким образом, система стабилизации любительских радиоуправляемых и полностью автономных летательных аппаратов, а также балансирующих роботов, может быть достаточно легко построена при помощи акселерометра, гироскопа и комплементарного фильтра, объединяющего их показания. Применение комплементарного фильтра не требует от контроллера машины большой вычислительной мощности и позволяет добиться достаточно качественной стабилизации полета или балансирования даже при использовании таких «легких» платформ как Arduino и TI LaunchPad MSP430.

Применение комплементарного фильтра и фильтра Калмана

#include <LiquidCrystal_I2C.h>

#include <Wire.h>

#include "Kalman.h"

#include <LiquidCrystal_I2C.h>

LiquidCrystal_I2C lcd(0x27,16,2);

Kalman kalmanX;

Kalman kalmanY;

uint8_t IMUAddress = 0x68;

/* IMU Data */

int16_t accX;

int16_t accY;

int16_t accZ;

int16_t tempRaw;

int16_t gyroX;

int16_t gyroY;

int16_t gyroZ;

double accXangle; // Angle calculate using the accelerometer

double accYangle;

double Xkomp;

double Ykomp;

double temp;

double gyroXangle = 180; // Angle calculate using the gyro

double gyroYangle = 180;

double compAngleX = 180; // Calculate the angle using a Kalman filter

double compAngleY = 180;

double kalAngleX; // Calculate the angle using a Kalman filter

double kalAngleY;

uint32_t timer;

void setup() {

Serial.begin(115200);

Wire.begin();

Serial.begin(9600);

lcd.init();

lcd.backlight();

i2cWrite(0x6B,0x00); // Disable sleep mode

kalmanX.setAngle(180); // Set starting angle

kalmanY.setAngle(180);

timer = micros();

}

void loop() {

/* Update all the values */

uint8_t* data = i2cRead(0x3B,14);

accX = ((data[0] << 8) | data[1]);

accY = ((data[2] << 8) | data[3]);

accZ = ((data[4] << 8) | data[5]);

tempRaw = ((data[6] << 8) | data[7]);

gyroX = ((data[8] << 8) | data[9]);

gyroY = ((data[10] << 8) | data[11]);

gyroZ = ((data[12] << 8) | data[13]);

/* Calculate the angls based on the different sensors and algorithm */

accYangle = (atan2(accX,accZ)+PI)*RAD_TO_DEG;

accXangle = (atan2(accY,accZ)+PI)*RAD_TO_DEG;

double gyroXrate = (double)gyroX/131.0;

double gyroYrate = -((double)gyroY/131.0);

gyroXangle += kalmanX.getRate()*((double)(micros()-timer)/1000000); // Calculate gyro angle using the unbiased rate

gyroYangle += kalmanY.getRate()*((double)(micros()-timer)/1000000);

kalAngleX = kalmanX.getAngle(accXangle, gyroXrate, (double)(micros()-timer)/1000000); // Calculate the angle using a Kalman filter

kalAngleY = kalmanY.getAngle(accYangle, gyroYrate, (double)(micros()-timer)/1000000);

Xkomp=(1-0.05)* gyroX + 0.05* accX;

Ykomp=(1-0.05)* gyroY + 0.05* accY;

timer = micros();

lcd.setCursor (0,0);

lcd.print ("X=");

lcd.print (kalAngleX,0);

lcd.print (" Y=");

lcd.print (kalAngleY,0);

delay (100);

lcd.clear ();

Serial.println();

Serial.print("X:");

Serial.print(kalAngleX,0);

Serial.print(" ");

Serial.print("Y:");

Serial.print(kalAngleY,0);

Serial.println(" ");

// The accelerometer's maximum samples rate is 1kHz

}

void i2cWrite(uint8_t registerAddress, uint8_t data){

Wire.beginTransmission(IMUAddress);

Wire.write(registerAddress);

Wire.write(data);

Wire.endTransmission(); // Send stop

}

uint8_t* i2cRead(uint8_t registerAddress, uint8_t nbytes) {

uint8_t data[nbytes];

Wire.beginTransmission(IMUAddress);

Wire.write(registerAddress);

Wire.endTransmission(false); // Don't release the bus

Wire.requestFrom(IMUAddress, nbytes); // Send a repeated start and then release the bus after reading

for(uint8_t i = 0; i < nbytes; i++)

data [i]= Wire.read();

return data;

}

Джойстик

Для плат Arduino существуют модули аналогового джойстика, как правило, имеющие ось X, Y и кнопку - ось Z. Джойстик позволяет более плавно и точно отслеживать степень отклонения от нулевой точки. А помимо удобства по сравнению с кнопками, это позволяет реализовывать более совершенные интерфейсы. К примеру, при изменении какого-либо значения в меню, можно написать программу таким образом, что чем сильнее отклонена ось джойстика, тем быстрее изменяется значение переменной. Например, нам необходимо изменить значение от 0 до 2000 с шагом в 1. Представьте, сколько раз вам потребовалось бы нажимать кнопку или писать специальный алгоритм, скажем при длительности нажатия больше 3 сек прибавлять изменять шаг на 10 или 100. А при использовании джойстика это можно реализовать намного проще.

const int POS_Y_PIN = 5;

const int POS_X_PIN = 4;

const int BUTTON_PIN = 2;

const int MAX_POS = 1023; // VRx и VRy выдают значения от 0 до 1023

const int MAX_ANGLE = 180;

void setup()

{

Serial.begin(9600);

}

void loop()

{

int yVal = analogRead(POS_Y_PIN);

int xVal = analogRead(POS_X_PIN);

float yAngle = 1.0 * yVal * MAX_ANGLE / MAX_POS; // Переводим выходные данные VRy в угол наклона джойстика (от 0 до 180)

float xAngle = 1.0 * xVal * MAX_ANGLE / MAX_POS; // Аналогично VRx

boolean isNotClicked = digitalRead(BUTTON_PIN); // Считываем не было ли нажатия на джойстик

Serial.print("Horisontal angle = ");

Serial.println(xAngle);

Serial.print("Vertical angle = ");

Serial.println(yAngle);

if (!isNotClicked)

{

Serial.println("Clicked");

} else

{

}

delay(1000);

}

Открыв монитор порта, мы видим значения которые выдает джойстик (рис. 30). Опираясь на эти данные уже можно собрать что-то интересное.

Рис. 30. Данные полученные с джойстика